Jarak dalam Ruang Bidang Datar {Bahan Ajar,Matematika Wajib XII, Semester Ganjil}
JARAK TITIK KE TITIK DALAM RUANG BIDANG DATAR
Konsep Jarak Titik ke Titik
Untuk memahami konsep jarak antara dua titik, mari kita perhatikan dua masalah berikut.
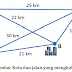
Bangun berikut merepresentasikan kota-kota yang terhubung dengan jalan. Titik merepresentasikan kota dan ruas garis merepresentasikan jalan yang menghubungkan kota.
Faisal berencana menuju kota C berangkat dari kota A. Tulis kemungkinan rute yang ditempuh Faisal dan tentukan panjang rute-rute tersebut. Rute manakah yang terpendek? Menurut pendapat kalian berapa jarak antara kota A dan C? Beri alasan untuk jawaban kalian.
Nah, untuk menjawab masalah di atas, kita akan membuat tabel kemungkinan rute yang bisa dilalui Faisal berikut ini.
|
No |
Kemungkinan rute
dari Kota A ke Kota
C |
Panjang Lintasan |
|
1 |
A ® C |
30 |
|
2 |
A ® B ® C |
21 + 18 = 39 |
|
3 |
A ® D ® C |
20 + 25 = 45 |
|
4 |
A ® B ® D ® C |
21 + 22 + 25 = 68 |
|
5 |
A ® D ® B ® C |
20 + 22 + 18 = 60 |
Tabel 1. Kemungkinan rute yang
ditempuh Faisal
Dari tabel di atas tampak bahwa rute terpendek dari Kota A ke Kota C adalah rute yang pertama: A ® C sepanjang 30 km.
Jadi, jarak antara kota A dan kota C adalah panjang lintasan terpendek yang menghubungkan antara kota A dan C, yaitu rute A ® C sepanjang 30 km.
Contoh 1.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 20 cm. Hitunglah jarak antara titik-titik berikut.
Jawab:
a. Jarak titik B ke F diwakili oleh panjang ruas garis (rusuk) BF. Jadi, jarak titik B ke F adalah 20 cm.
b. Jarak titik A ke D diwakili oleh panjang ruas garis (rusuk) AD. Jadi, jarak titik A ke D adalah 20 cm.
c. Jarak titik G ke H diwakili oleh panjang ruas garis (rusuk) GH. Jadi, jarak titik G ke H adalah 20 cm.
d. Jarak titik A ke C diwakili oleh panjang ruas garis AC. Ruas garis AC merupakan diagonal bidang alas ABCD.
e. Jarak titik H ke B diwakili oleh panjang ruas garis HB. Ruas garis HB merupakan diagonal ruang kubus ABCD.EFGH.
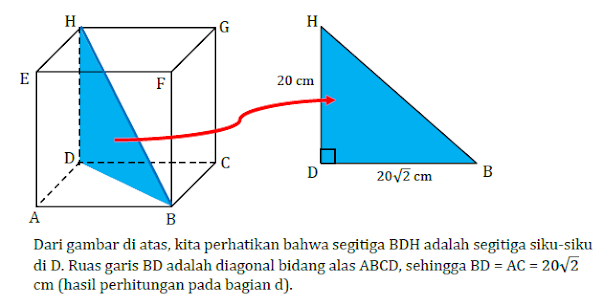












Tidak ada komentar